
Nadmiar przechyłki
Artykuł ten jest kontynuacją zagadnienia opisanego w artykule „Niedomiar przechyłki” i warto zachować taką kolejność ich lektury.
Po większości linii kolejowych pociągi poruszają się ze zróżnicowanymi prędkościami maksymalnymi. Zazwyczaj pociągami szybszymi są pociągi pasażerskie, a pociągami wolniejszymi – pociągi towarowe. W przypadku pociągów wolniejszych może pojawić się zjawisko nazywane nadmiarem przechyłki, w polskiej literaturze opisywane tradycyjnie za pomocą wielkości niezrównoważonego przyspieszenia dośrodkowego.
Zagadnienie opracowano w oparciu o artykuł, który ukaże się w najnowszym numerze (19/2015) Archiwum Instytutu Inżynierii Lądowej: Kosicki D., Plucińska E.: Projektowanie układu geometrycznego linii kolejowych w planie w świetle nowelizacji przepisów krajowych.
Na rysunku 1 przedstawiono układ przyspieszeń pociągu poruszającego się po łuku z przechyłką z małą prędkością. Zjawisko nadmiaru przechyłki wystąpi w sytuacji, w której wektor wypadkowego przyspieszenia pociągu będzie odchylony od pionu o kąt mniejszy niż kąt prostej prostopadłej do płaszczyzny toru [1]. Symbolem e oznaczono szerokość toru, przyjmowaną w obliczeniach jako rozstaw osiowy szyn, równy 1,5 m. Odległość p jest wielkością pomocniczą, wykorzystywaną w obliczeniach.
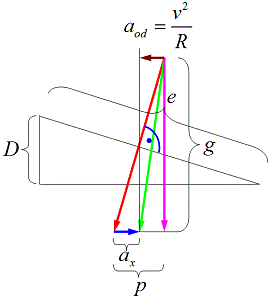
Rys. 1. Układ przyspieszeń pociągu poruszającego się po łuku z przechyłką z małą prędkością.
Na podstawie zależności przedstawionych na rysunku 1 (podobieństwo trójkątów), a także przyjmując przybliżenie, że dla małych kątów sinα ≈ tgα, można utworzyć układ równań:
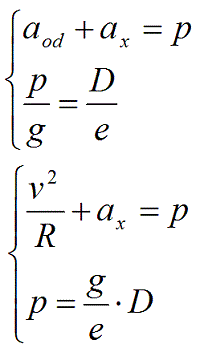
Stąd otrzymujemy wzór na niezrównoważone przyspieszenie dośrodkowe:
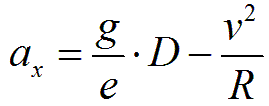
Zauważmy, że istnieje taka wartość przechyłki równa (D – E), że wypadkowa siła działająca na tabor będzie prostopadła do płaszczyzny toru [4]. Wartość E jest właśnie nadmiarem przechyłki (cant excess), czyli wartością wskazującą, o ile należy zmniejszyć przechyłkę, aby w pełni równoważyła ona siłę odśrodkową, czyli aby wypadkowa siła działająca na tabor była prostopadła do płaszczyzny toru [5]. Rozważania analogiczne jak w artykule „Nadmiar przechyłki” pozwalają wyprowadzić następujący wzór:
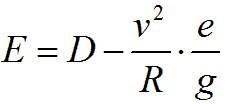
Przykład obliczeniowy
Obliczyć wartość niezrównoważonego przyspieszenia dośrodkowego pociągu poruszającego się z prędkością 60 km/h po łuku o promieniu R=1200 m i przechyłce D=80 mm. Następnie dla tych samych danych obliczyć niedomiar przechyłki i porównać wyniki.
Obliczenie niezrównoważonego przyspieszenia dośrodkowego:
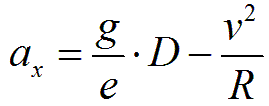
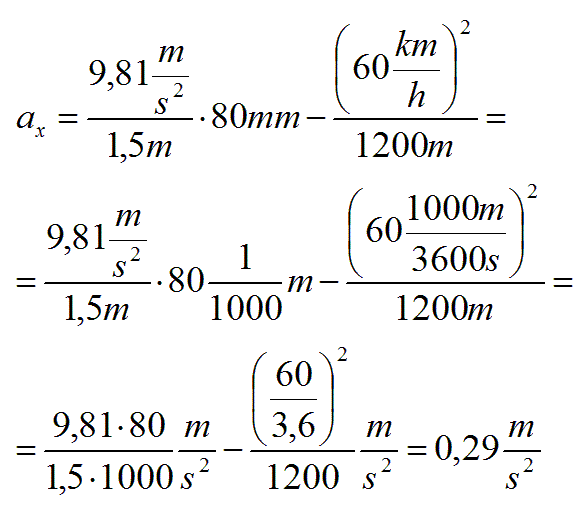
Obliczenie nadmiaru przechyłki:
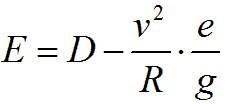
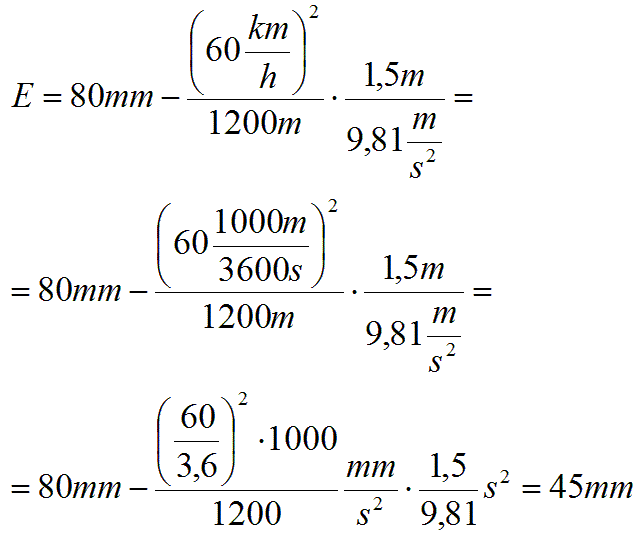
Sprawdzenie:
![]()
Wartości graniczne
W tabeli 1 przedstawiono wartości graniczne nadmiaru przechyłki i odpowiadającego mu niezrównoważonego przyspieszenia dośrodkowego według trzech aktów prawnych:
– Rozporządzenia w sprawie warunków technicznych, jakim powinny odpowiadać budowle kolejowe i ich usytuowanie z 1998 roku [8],
– nowelizacji ww. Rozporządzenia, z 2014 roku [7],
– normy PN-EN13803 [5], do której odwołuje ww. nowelizacja Rozporządzenia w przypadku obliczeń prowadzonych dla linii objętych procedurą oceny zgodności z wymaganiami zasadniczymi dla interoperacyjności systemu kolei.
Tab. 1. Wartości graniczne nadmiaru przechyłki i niezrównoważonego przyspieszenia dośrodkowego
|
Podstawa obliczeń |
Wartość graniczna |
|
|
Nadmiar przechyłki [mm] |
Niezrównoważone przyspieszenie dośrodkowe [m/s2] |
|
|
Obciążenie przewozami w Tg/rok: 0 ≤ T < 5 |
||
|
Rozporządzenie [8] |
91 |
0,60 |
|
Nowelizacja rozporządzenia [7] |
110 |
0,72 |
|
Norma [5] |
110 |
0,72 |
|
Obciążenie przewozami w Tg/rok: 5 ≤ T < 10 |
||
|
Rozporządzenie [8] |
76 |
0,50 |
|
Nowelizacja rozporządzenia [7] |
94 |
0,62 |
|
Norma [5] |
110 |
0,72 |
|
Obciążenie przewozami w Tg/rok: 10 ≤ T < 15 |
||
|
Rozporządzenie [8] |
61 |
0,40 |
|
Nowelizacja rozporządzenia [7] |
79 |
0,52 |
|
Norma [5] |
110 |
0,72 |
|
Obciążenie przewozami w Tg/rok: 15 ≤ T < 20 |
||
|
Rozporządzenie [8] |
45 |
0,30 |
|
Nowelizacja rozporządzenia [7] |
64 |
0,42 |
|
Norma [5] |
110 |
0,72 |
|
Obciążenie przewozami w Tg/rok: 20 ≤ T |
||
|
Rozporządzenie [8] |
30 |
0,20 |
|
Nowelizacja rozporządzenia [7] |
48 |
0,32 |
|
Norma [5] |
110 |
0,72 |
Praktyczna postać wzorów
Wyprowadzone w niniejszym artykule wzory warto przekształcić do postaci łatwiejszej w praktycznych zastosowaniach:
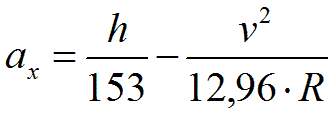
ax – niezrównoważone przyspieszenie dośrodkowe [m/s2],
v – prędkość, dla której obliczana jest wartość ax [km/h],
R – promień łuku poziomego [m],
h – przechyłka [mm].
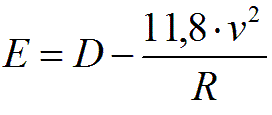
E – nadmiar przechyłki [mm],
v – prędkość, dla której obliczana jest wartość E [km/h],
R – promień łuku poziomego [m],
D – przechyłka [mm].
Literatura
[1] Bałuch H., Bałuch M.: Układy geometryczne toru i ich deformacje, KOW, Warszawa 2010.
[2] Decyzja 2011/275/UE Komisji z dnia 26 kwietnia 2011 r. dotycząca technicznej specyfikacji interoperacyjności podsystemu „Infrastruktura” transeuropejskiego systemu kolei konwencjonalnych.Dz. U. L126 z 14.5.2011, str. 53-120.
[3] Drogi kolejowe. Praca zbiorowa pod red. J. Sysaka. PWN, Warszawa 1982.
[4] Massel A.: Projektowanie linii i stacji kolejowych, KOW, Warszawa 2010.
[5] Norma PN-EN 13803-1:2010 Kolejnictwo – Tor – parametry projektowania toru w planie – Tor o szerokości 1435 mm i większej – Część 1: Szlak.
[6] Norma PN-EN 13803-2+A1:2010 Kolejnictwo – Tor – Parametry projektowania toru w planie – Tor o szerokości 1435 mm i większej – Część 2: Rozjazdy, skrzyżowania i inne porównywalne przypadki z nagłymi zmianami krzywizny.
[7] Rozporządzenie Ministra Infrastruktury i Rozwoju z dnia 5 czerwca 2014 r. zmieniające rozporządzenie w sprawie warunków technicznych, jakim powinny odpowiadać budowle kolejowe i ich usytuowanie (Dz.U. 2014 nr 0 poz. 867).
[8] Rozporządzenie Ministra Transportu i Gospodarki Morskiej z dnia 10 września 1998r. w sprawie warunków technicznych, jakim powinny odpowiadać budowle kolejowe i ich usytuowanie (Dz.U. 1998 nr 151 poz. 987).
[9] Warunki techniczne utrzymania nawierzchni na liniach kolejowych – Id-1, PKP Polskie Linie kolejowe, Warszawa 2005.

